Parallelized Suffix Array Construction: Final Writeup
Summary
We implemented an optimized suffix array construction algorithm (SACA) for distributed cluster computing. This uses OpenMP to achieve parallelism within a core, and OpenMPI to do node-to-node communication. We implemented two different algorithms. The first, pDC3, is a classic suffix array construction algorithm which we adapted and implemented for cluster computing. The second, pCSS, is a novel algorithm we developed for suffix array construction. It has low inter-node communication complexity and scales well across cores. We tested the algorithms on the Carnegie Mellon Latedays cluster, varying from 1 to 8 nodes.
What is a Suffix Array?
A suffix array is a data structure which stores the suffixes of a string in sorted order. Let S be a length n string. It stores an array which at entry i stores the starting index of the lexicographically ith smallest suffix (the suffix at index i is S[i ... n - 1]). The suffix array is related to the suffix tree data structure, but uses a smaller memory footprint (approximately 5 times less) and has the benefit of cache locality.
Suffix arrays are used in numerous compression algorithms, and speed up many string operations, like substring search. Hence increased performance from either multithreaded, distributed, or CUDA accelerated programs greatly impacts the ability to work and operate efficiently on large data sets.
There are two common algorithms for suffix array construction. The DC3 algorithm contracts the problem and solves a subproblem of size 2/3, and uses to solution to create the suffix array in linear time. It works by carefully selecting a subset of suffixes and sorts the suffixes and additional data. We implemented a distributed version of this algorithm.
The other algorithm, prefix doubling, works by sorting fixed sized suffixes in rounds, doubling in size each round. It first sorts by 1 character, then 2 characters, then 4 characters, and so on. It often uses radix sorting.
The most expensive part of the algorithm is the sort. The algorithm requires some type of sort to arrange the suffixes. Suffixes can be linear in the size of the array, so the type of sort depends on the algorithm, i.e, the number of characters per suffix the algorithm uses. An algorithm which uses too much of the suffix may end up using too much memory, so there needs to be balance between memory usage and speed. Once we begin to parallelize this, the algorithms will require significant amounts of communication between nodes, so this needs to be taken into account.
These are the most common applications.
pDC3 (Parallel Difference Cover modulo 3)
Algorithm
The sequential Difference Cover modulo 3 (DC3) algorithm for constructing suffix arrays is as follows:
- For each index in the string, get the triple of three consecutive characters starting at that index.
- Sort these triples. If these are not unique, then recursively solve for the suffix array of these triples of the corresponding indices i where i mod 3 is not zero. This is a subproblem of size 2/3 of the original input.
- Using the result of the recursive call to construct 3 arrays containing information about the positions of suffixes for indices which are 0,1,2 mod 3.
- Merge these three arrays using a carefully chosen comparator.
For large datafiles on the order of several gigabytes, it is not memory efficient to attempt to compute the suffix array on a single machine. We thus aim to construct the suffix array in parallel across several machines. The bulk of the work consists several rounds of sorting, which can be parallelized to improve efficiency even when the datafiles are not huge. In addition, the algorithm iterates over arrays several times, which is obviously parallelizable.
Parallelization
We wrote our parallel implementation of the DC3 algorithm in C++ and used MPI to communicate across nodes on the Latedays cluster. To parallelize the algorithm, we spawned several processes on each node and gave roughly equal contiguous chunks of the input to each process.
We make a few changes to the sequential DC3 algorithm. Since merging is difficult to parallelize, we choose to sort everything instead of merging. In addition, instead of actually recursively calling our algorithm, we send all of the data to one node and run a sequential implementation (the SA-IS algorithm implemented by Yuta Mori). This was originally just for testing purposes; we were planning on expanding our implementation to recursively call itself. However, after timing our algorithm, it became clear that the runtime would be fairly poor even if the algorithm did recursively call itself. (This is discussed further in the Results section.) We thus chose not to complete the recursive implementation.
Much of the runtime lies in sorting and necessary communication. We were able to reduce the communication costs somewhat by representing our elements in a compact way, and we sped up sorting by writing fast comparison functions. (This is not entirely trivial because at one point in our algorithm we have four-tuples and five-tuples that need to be sorted with a non-lexicographic comparison function.)
pCSS (Parallel Cascading Suffix Sort)
Algorithm and Motivation
We decided to develop a new algorithm which is inspired from pDC3, prefix doubling, and other suffix sorting algorithms. We wanted to reduce the amount of inter-node MPI communication, as this was taking the bulk of the execution time for pDC3. pDC3 also had a high per-character memory overhead.
- Create an array of 8-length contiguous substrings (samples) for each position in the string.
- Sort the array of samples using a distributed sort.
- Now, all suffixes are sorted by the first 8-letters across the nodes. Therefore suffixes with different samples are sorted correct, but suffixes with the same samples may not be sorted. These are arranged contiguously. Find contiguous sequences of suffixes with equal samples in each node, and sort them using a simple sequential sort.
- Find contiguous sequences of suffixes with equal samples across nodes, and sort them.
Parallelization
We first assign contiguous chunks of the string to each processing node. Each node calculates its 8-length samples for each index in the string, for its individual part. We choose 8 simply since 8 characters can fit into a 64-byte long long datatype, and allows the string to have much higher entropy during the per-node sorting phase. These samples are sorted using sample sort. Once this is complete, we have a representation of the suffixes such that they are sorted by the first 8 characters.
However, substrings with equal samples are possibly unsorted. These lie contiguously. Hence, on each node, we search for contiguous sequences of equal samples. For each sequence, we sort the sequences of equal samples using a naive technique which just compares the suffixes at both positions. Hence the worst case runtime is large. The average case runtime, however is fairly small. It is possible to improve this using advanced techniques, but we did not pursue these.
Once we have sorted the sequences per node, we have to sort the contiguous sequences which lie at the boundary of nodes. This requires adjacent node communication. In the average case, this communication will be very small, or even nonexistent. After this, we have a fully sorted suffix array.
Optimizations and Performance
We use 64-byte integers to store the samples. This allows for easy sorting, as sorting is simply an integer sort and not a string sort. This makes it possible to replace sample sort which a possibly faster integer specific sort. All in all, this algorithm requires only 1 call to a multi-node sort. After this, the communication is minimal. So this substantially improves upon the communication complexity of pDC3. In addition, the sort in pCSS makes lightweight integer comparisons, where the comparators in the different sorts of pDC3 require much heavier comparators.
We only spawn 1 MPI process per node. To achieve inter-node parallelism, we use OpenMP. This allows us to spawn multiple threads per node and parallelize the local sorting across the individual portion of the string on the node. In addition, this allows the samplesort to take advantage of a multithreaded per-core sort. In samplesort, each processing element needs to locally sort its chunk of elements. As the granularity of processing elements are now nodes, we do this using OpenMP threads to parallelize the sort. GCC has parallel extensions through OpenMP, so we simply have to compile with parallel flags.
To find contiguous sequences of equal samples, we simply loop through the array. We utilize the multiple threads per node to split this into parallel searches. At the end, we have to look for contiguous sequences across threads, and then across nodes.
However, this method has its drawbacks. In the current implementation, if the string contains a large number of very long repeats, then the local sort on that sequence will be slow, since we are search through the entire suffix. However we argue that it is unlikely for this to happen over most strings, so the cost of this operation will be low. We can also tune the length of samples to improve the performance of low entropy strings. Importantly, this algorithm in its current implementation requires the entire string be accessible to each node. For our implementation, we simply loaded the string into each node. However we can reduce this cost with node communication. Each node needs access to the whole string during the local sorting phase, but this can be probably replaced with communicating with the appropriate node, instead of storing the whole string. The amount of computation during the local sorting is small, so we don't expect using node-to-node communication to substantially increase the cost.
Sorting
Sorting data across several nodes is a crucial part of both pDC3 and pCSS. To accomplish this, we wrote an implementation of samplesort in MPI and C++. Samplesort takes as input an array and a comparison function. The end result is that if the data from each processor is concatenated in order of processor ID, the concatenation is sorted. For p processors, the algorithm is as follows:
- Sample p-1 "splitting" points from the input data.
- Each processor samples some points from its local data.
- Gather all these local samples at one processor and pick the splitters based on these local samples. Sort these splitters.
- Broadcast the splitters to all the processors.
- Each processor partitions its local data into p buckets based on the splitters. Each bucket holds data that falls within an interval where the interval's endpoints are adjacent splitters. The buckets have the property that each element in bucket i is "less than" any element bucket j (where "less than" is defined by the input comparison function) if i is less than j.
- Give all the elements of bucket i to processor i and sort each bucket.
There was not much to optimize here. Most of the runtime comes from communication and two rounds of local sorting. We could not find any way to avoid this communication and sorting altogether. One of the rounds of sorting can be replaced by a multiway merge, which is asymptotically faster. However, our implementation of merging turned out to be slower than the original sort, so we did not use this in our final samplesort implementation.
For the granularity of calling samplesort across nodes in pCSS, as opposed to per process, we parallelized the local sorting by using GCC's parallel extensions . This is a parallel extension to GCC's algorithms using the OpenMP framework. This allowed full utilization of each node for local sorting.
Results
Measuring Results
We measured performance by finding the speedup of our algorithms compared to a sequential baseline implementation. We measure the time to construct the suffix array, not including the time it takes convert the read input textfile into a char array and to write the output suffix array. This also does not include the time for provisioning a cluster.
Experimental Setup
For our inputs, we generated files of random mixed-case English letters. We did this for sizes 1MB, 5MB, 10MB, 20MB, 50MB, 100MB, 250MB, 500MB, 750MB, and 1GB. In addition, we use real world datasets from Guy Blelloch's PBBS (Problem Based Benckmark Suite), namely etext, chr22, wikisamp, and trigrams.
Baseline
To compare the performance our of parallel algorithms, we use an Yuta Mori's implementation of the SA-IS algorithm by Nong, Zhang & Chan (2009) . This uses the method of induced sorting to construct suffix arrays. This implementation is commonly used as a baseline in other suffix array papers and it one of the fastest (if not the fastest) single-threaded implementation. It has both linear construction time and optimal memory usage.
| Dataset | Runtime (s) |
|---|---|
| trigrams (42KB) | 0.0001 |
| wikisamp (8.5MB) | 1.54 |
| chr22.dna (8.1MB) | 1.44 |
| etext (28MB) | 5.46 |
| random 1MB | 0.16 |
| random 5MB | 0.83 |
| random 10MB | 1.52 |
| random 20MB | 3.06 |
| random 50MB | 7.89 |
| random 100MB | 16.00 |
| random 250MB | 40.69 |
| random 500MB | 81.73 |
| random 750MB | 130.06 |
| random 1GB | 205.00 |
Data
| Dataset | 1 Node Runtime (s) | 2 Node Runtime (s) | 4 Node Runtime (s) | 8 Node Runtime (s) |
|---|---|---|---|---|
| trigrams | 0.04256 | 0.069251 | 0.067058 | 0.06885 |
| wikisamp | 1.110653 | 1.353469 | 0.899169 | 0.599915 |
| chr22.dna | 1.099506 | 1.311307 | 0.858363 | 0.574447 |
| etext | 2.843792 | 4.105355 | 2.768228 | 1.626782 |
| random 1MB | 0.164474 | 0.188504 | 0.168423 | 0.128414 |
| random 5MB | 0.730067 | 0.79204 | 0.568226 | 0.374353 |
| random 10MB | 1.323709 | 1.478898 | 1.026515 | 0.665979 |
| random 20MB | 2.064725 | 2.944016 | 1.951967 | 1.219765 |
| random 50MB | 4.244969 | 6.467543 | 4.775463 | 2.739247 |
| random 100MB | 7.209381 | 11.327291 | 8.386905 | 5.078551 |
| random 250MB | 19.277768 | 28.263648 | 19.477082 | 11.092358 |
| random 500MB | Out of memory | 54.081576 | 40.688515 | 29.501891 |
| random 750MB | Out of memory | Out of memory | 59.407972 | 38.01542 |
| random 1GB | Out of memory | Out of memory | 79.404072 | 51.243268 |
pDC3 Performance Analysis
Graphs
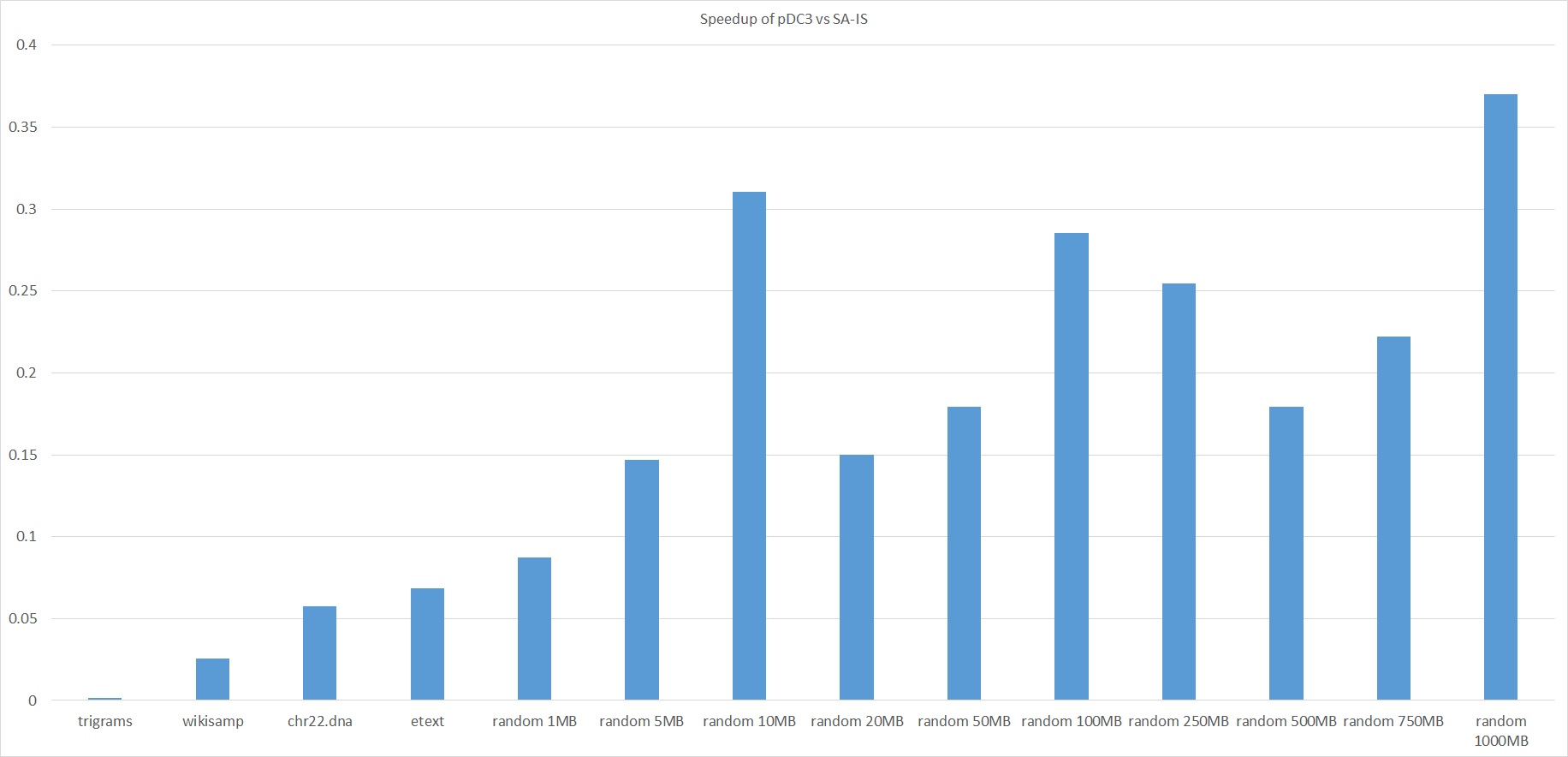
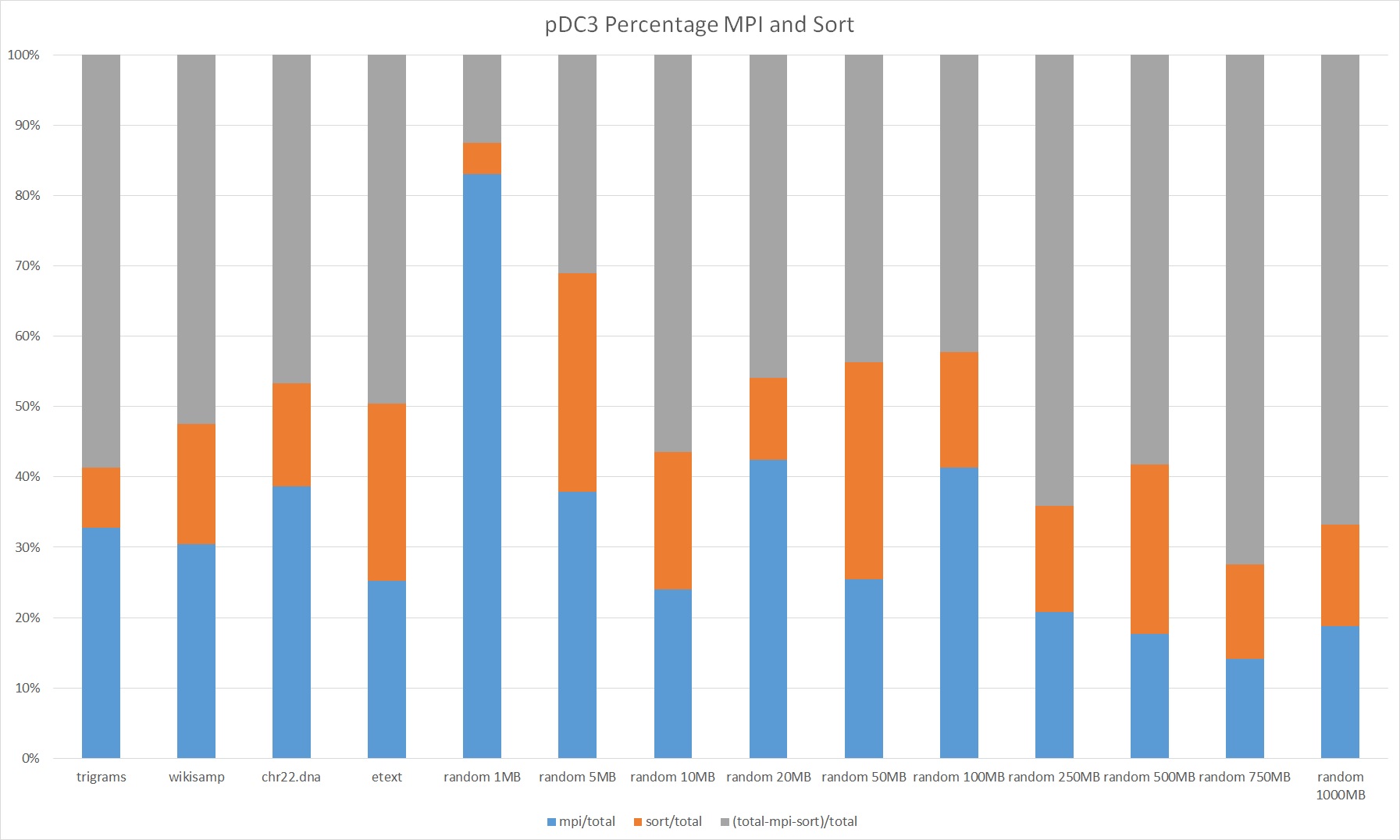
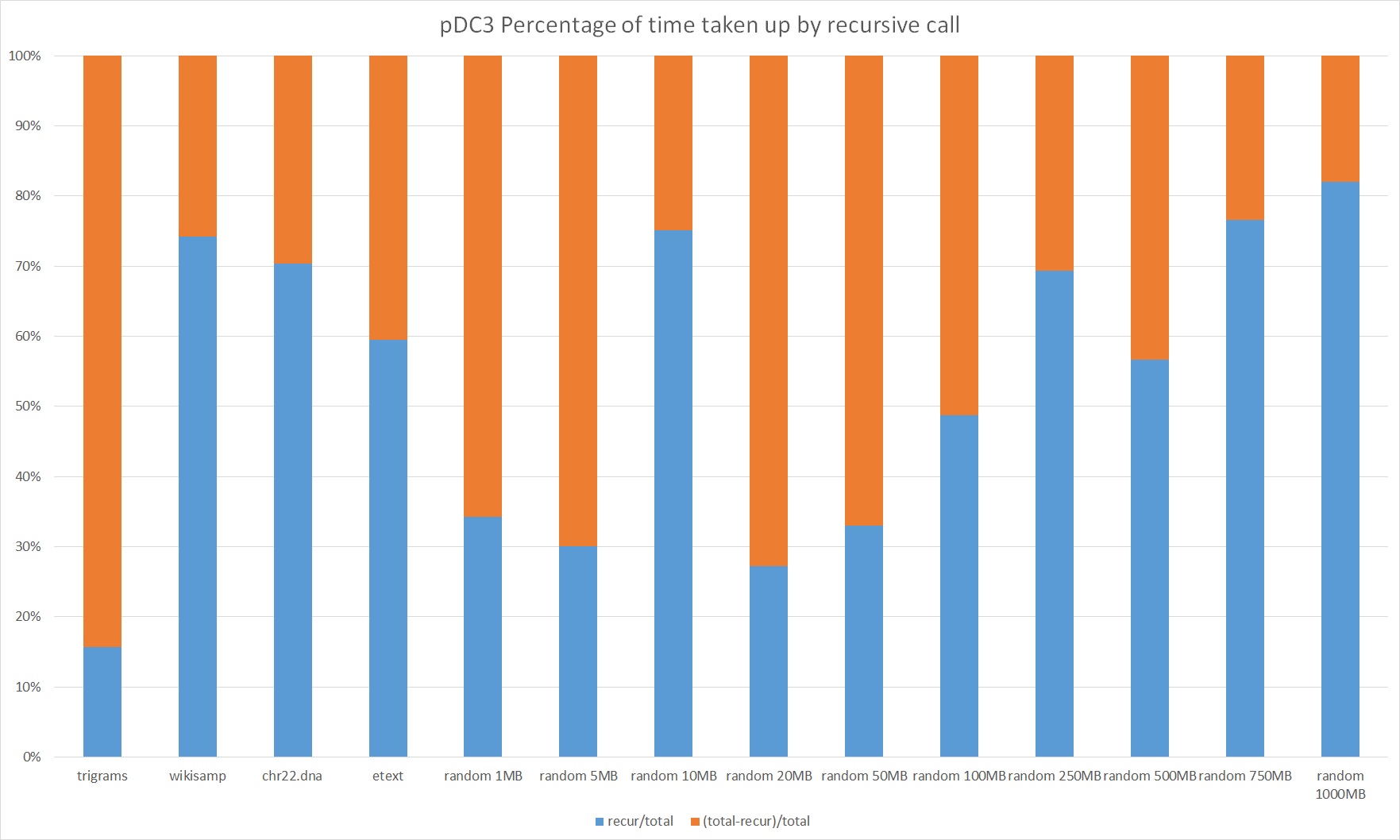
Analysis
We found that almost all of the run time of pDC3 comes from MPI communication, calls to STL sort in the implementation of samplesort, and calling SA-IS.
The algorithm is data-transfer-bound and memory-bound. This is not hard to guess based on the fact that pDC3 consists mostly of writing data and sending it to other processors with very little arithmetic involved. We verified this guess by reducing the size of the datatypes used and observing that the MPI communication times and sorting times decreased dramatically.
It is difficult to optimize MPI communication and local sorting, but what about the call to SA-IS? At first, this seems like this is an obvious bottleneck to the performance of pDC3 since we funnel all the data to a single node and run a single-threaded algorithm. Indeed, our original plan was to call pDC3 recursively instead of calling SA-IS.
However, our results suggest that we would not gain any performance by doing so until we reach inputs of over 750MB in size. Experimentally, the implementation seems to scale roughly linearly with the problem size. If the size of initial input is n, the sum of the problem sizes of the recursive calls is 3n. So if the additional runtime at each recursive call is about cn where c is some constant, we expect the total runtime to be roughly 3cn. But in reality, the actual runtime would be even worse because the recursive call runs on larger datatypes (since triplets of characters don't fit in a C char), which is terrible for data transferral and memory access. The conclusion is that our algorithm probably would not gain any performance from removing the SA-IS call until the amount of time taken up by the recursive call is significantly more than twice the amount of time taken up by everything else. In our experiments running on four nodes, this doesn't occur until the input size is on the order of a gigabyte.
Considering that our implementation is already much slower than SA-IS is, we decided that this was not a worthy avenue to pursue further.
pCSS Performance Analysis
Graphs
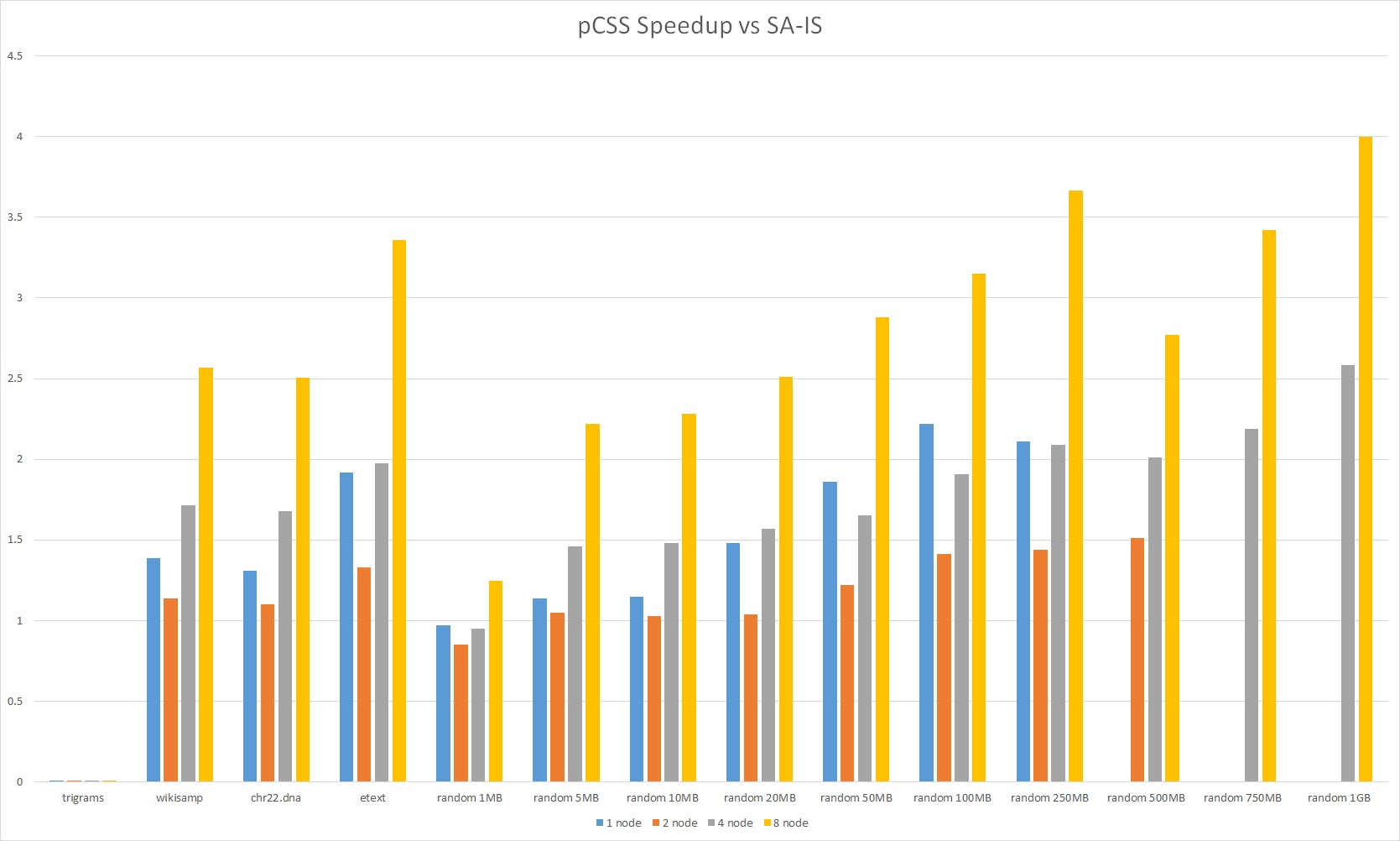
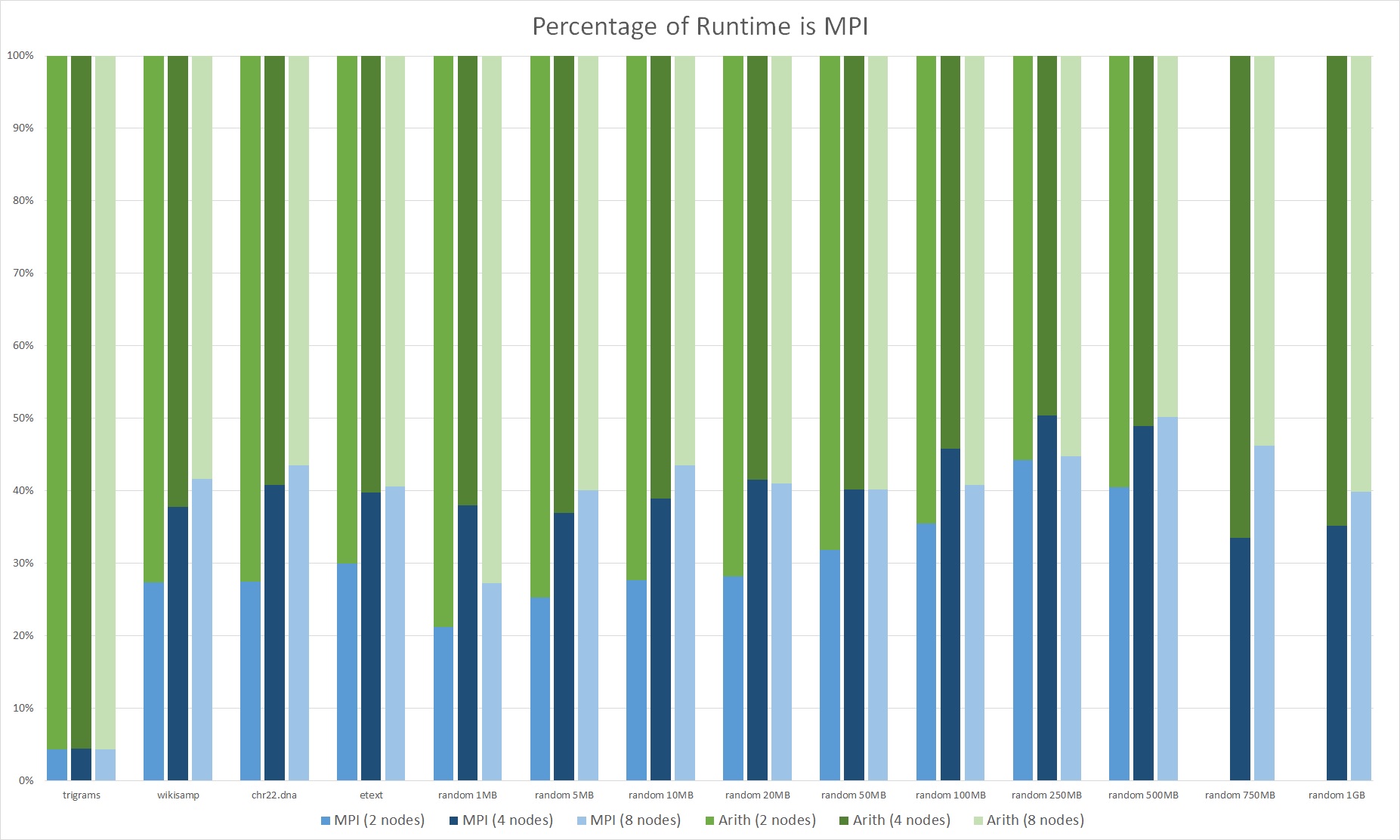
Analysis
Due to the reduced communication costs and less expensive sort, pCSS performed significantly better than pDC3. It was able to achieve 3-4x speedup over SA-IS on 8 nodes for the large datasets. Even for real world inputs, our algorithm performed well, and hence our assumption about large number of equal and long strings held. We also observe increasing speedup and we increase the number of nodes, so the algorithm seems to scale well.
As discussed in the last graph, a major component of the algorithm is still communication costs, accounting for 40% of the runtime. This is a similar percentage to pDC3. It is large percentage since we also improved the computation complexity significantly. Since our test interface, the Latedays cluster, uses ethernet connections between nodes, and not a high-speed interconnection network, we suspect that we can limit the impact of communication by using a better linked distributed system.
We can split the algorithm into 4 main components. The first component is constructing the sample array. The second component is performing the distributed sort over all nodes over the sample array. The third component is perform local per-node sample-correction sorts. The last component is extracting the suffix array indices from the sorted sample array. By analyzing the runtime of each component, we found that that pCSS spends 97% of its runtime performing the samplesort. So the primary method of improving this algorithm would be improving the performance and communication complexity of the sort. As discussed before, the distributed sort is over integers. Hence we do not need a comparison based sort and we can replace it with a possibly more efficient integer-specific sort of radix sort.
Our sample sort implementation works by performing local sorts on each node, and then doing a multi-way merge by redistributing data across nodes. Within the samplesort implementation, we used GNU parallel extensions to perform multithread local sort on each node, so this is likely to be already highly optimized. Therefore, the only thing left is performing multiway merge and moving elements across nodes, which becomes bottlenecked on the interconnect speed.
Machine Choice
Our problem focused on constructing suffix arrays on large datasets. Hence using GPUs is not viable since they have very limited memory. In addition, suffix array construction is not data parallel. As discussed, the algorithms we discussed would work well on CPU's, as shown by our 1 node results. But the goal was to build large suffix arrays which cannot fit on a single CPU, so using a distributed cluster was the best option.
Future work
Given that our algorithms transfer so much data and use so much memory, it is likely that we can achieve some speedup by compressing data. Since our algorithms are not compute-bound, the costs to compress and decompress data could be acceptable.
References
An excellent source which provides background and a complete taxonomy of the types of suffix array construction algorithms (SACAs) and the varying implementations over the past 30 years is the following paper by Puglisi et. al: Taxonomy of Suffix Array Construction.
The papers were useful in learning about CPU based suffix array construction:
- Parallel Suffix Array Construction by Accelerated Sampling
- An Elegant Algorithm for the Construction of Suffix Arrays
- Parallel DC3 Algorithm for Suffix Array Construction on Many-Core Accelerators
- Parallel Lightweight Wavelet Tree, Suffix Array and FM-Index Construction
These were the papers were referenced for distributed suffix array construction:
Work Distribution
Equal work was done by both members of the group.